Infix To Postfix Rules
infix postfix rules wallpaperKeep the expression ABC in your mind. Infix notation is the notation commonly used in arithmetical and logical formulae and statements.
Assume the fully parenthesized version of the infix expression 2.
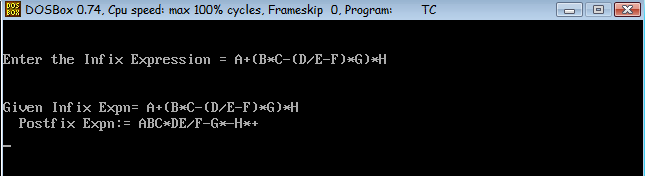
Infix to postfix rules. You will need to design implement and test a utility class Notation to support - Infix to postfix conversion of an expression Postfix to infix conversion. If the stack is empty or contains a left parenthesis on top push the incoming operator onto the stack. Infix to postfix conversion Scan through an expression getting one token at a time.
Converting Infix to Postfix We know that the infix expression AB C-D is equivalent to the postfix expression ABCD-. If the incoming symbol is a left parenthesis push it on the stack. In Postfix expressions operators come after the operands.
Lets convert the former to the latter. The order of evaluation of operators is always left-to-right and brackets cannot be used to change this order. The postfix expressions can be evaluated easily using a stack.
Conversion of infix to postfix expression can be done elegantly using two precedence function. A B C Given infix form C B A Convert the addition C B A Convert the multiplication. The rules for operators are different.
Push onto Stack and add to the end of X. Postfix notation also known as Reverse Polish notation. Evaluate the postfix expression by using a stack to store operands and then pop them when an operator is reached.
We have to know the rules of operator precedence in order to convert infix to postfix. Let X is an arithmetic expression written in infix notation. First rule of algorithm is that if we find the operand in the infix form put it in the postfix form.
Convert the infix form to postfix using a stack to store operators and then pop them in correct order of precedence. We will cover postfix expression evaluation in a separate post. A summary of the rules follows.
The cannot be inserted in the postfix expression until its second operand has been scanned and inserted. It is characterized by the placement of. Below are an infix and respective Postfix expressions.
The order of evaluation of operators is always left-to-right and bracketscannot be used to change this order. Operators are written after their operands. It is better to convert the expression to postfixor prefix form before evaluation.
Postfix expression of example above will be A B C D. Infix Postfix converter. This tool gives you a way to change between infix seen normally in most writing and post fix also known as reverse polish notation or Polish postfix notation which is used in some HP calculators such as the 9100A and HP-35.
Scan the infix expression from left to right. Rules for Infix to postfix using stack DS Scan Expression from Left to Right Print OPERANDs as the arrive If OPERATOR arrives Stack is empty push this operator onto the stack IF incoming OPERATOR has HIGHER precedence than the TOP of the Stack push it on stack IF incoming OPERATOR has LOWER. Move all operators so that they replace their corresponding right part of parenthesis 3.
Scan X from left to right and repeat Step 3 to 6 for each element of X until the Stack is empty. Print operands as they arrive. Each operator is assigned a value larger value means higher precedence which depends upon whether the operator is inside or outside the stack.
A B A B As mentioned in the above example the Postfix expression has the operator after the operands. Infix Postfix Notations. The corresponding expression in postfix form is.
General Infix-to-Postfix Conversion We need to develop an algorithm to convert any infix. Rules for converting Infix expression to a Postfix Expression. The infix expression given aboveis equivalent toA B C D.
This algorithm finds the equivalent postfix expression Y. Infix to Postfix using different Precedence Values for In-Stack and Out-Stack. Operators are used after their operands for example to add 3 and 4 instead of writing 3 4 which is infix expression postfix expression will be 3 4.
